A gas exploration well has 13-3/8” casing set at 6200 ft. Design a 9-5/8” casing string to be set at 10,400 ft in 73 pcf mud that will be subjected, in the event of a kick, to a formation pressure gradient of 0.57 psi/ft from the next hole drilled to a TD of 13,900 ft.
The 9-5/8” casing in stock at the pipe yard is:
| Grade | Weight Ib/ft | Collapse Rating | Burst Rating | Tensile LT&C 1000 lb | Tensile Butt 1000 lb |
C-75 | 43.5 | 3750 | 5930 | 776 | 1016 |
| L-80 | 47 | 4750 | 6870 | 905 | 1161 |
| C-95 | 53.5 | 8960 | 9410 | 1220 | 1458 |
Collapse
At the surface collapse pressure = 0
At the casing shoe collapse pressure = (73 pcf x 10,400 ft)/144 = 5272 psi
It is obvious that the 53.5# will have to be run on bottom. The question is how much 53.5# do we need to run before we can switch over to the less expensive lighter weight casing.
Taking the collapse figure for the 47# we can calculate the deepest point to which this weight casing can be run and still satisfy the collapse requirements with the1.125 SF.
(4750 psi/1.125) ÷ (73 pcf/144 in2/ft2) = 8,330 ft
Doing the same for the 43.5# casing we get:
(3750psi/1.125)÷(73pcf/144in2/ft2)=6,575 ft.
Therefore designing the casing string for collapse gives us:
- 10,400 ft – 8,330 ft 53.5# C-95
- 8,330 ft – 6,575 ft 47# L-80
- 6,575 ft – surface 43.5# C-75
Burst:
The 9-5/8 in casing will be subjected, in the event of a kick, to a formation pressure of:
0.57 psi/ft x 13,900 ft = 7,923 psi
The burst pressure at the shoe is: internal pressure – external pressure or:
Burst at shoe = [Pf – (TD – CSD) x G] – [CSD x (Mud Gradient)]
Where:
CSD is casing setting depth = 10,400 ft, and
Mud Gradient is 73 pcf/144 in2/ft2 = 0.507 psi/ft
A gas kick is expected for this well, since G is 0.1 psi/ft, we get:
Burst at shoe = [7923 psi – ((13,900 ft-10,400 ft) x 0.1 psi/ft)]-(10,400 ft x 0.507 psi/ft)) = 2300 psi
Burst at the surface is = Pf – (TD x G) or: 7923 psi – (13,900 ft x 0.1 psi/ft) = 6533 psi x 1.1 S.F. = 7186 psi
By comparing 7186 psi with what the burst rating for 43.5# C-75 of 5930 psi, we can see that some heavier weight 47# L-80 and 53.5# C-95 casing is required for the top of the string instead of the 43.5#.
We can calculate the amount required by each with:
(Burst at surface – casing burst rating)/mud gradient = (7186 – 5930) / (73/144) = 2,478’
and since the burst rating for 47# L-80 is 6870 psi which is less than 7186 psi we then calculate how much 53.5# C-95 is required at the surface in order to satisfy the burst requirement.
(7186 – 6870) ÷ (73/144) = 623 ft
Therefore, from the previous collapse design we adjust the design for burst considerations and we can see that 47# and 53.5# casing is needed at the top of the string. We now have a casing design, in the order going in the hole, of:
- 10,400 ft – 8,330 ft 53.5# C-95
- 8,330 ft – 6,575 ft 47# L-80
- 6,575 ft – 2,478 ft 43.5# C-75
- 2,478 ft – 623 ft 47# L-80
- 623 ft – surface 53.5# C-95
Next we need to check the tensile strength of the design to ensure that this design will pass the tensile design criteria.
Tension
The suitability of the selected design will be investigated by considering the total tensile load resulting from the buoyant weight of the string.
The buoyancy factor for 73 pcf mud is: Fb = 1 – (73/490) = 0.849
Starting from the bottom, the weight carried by each section is as follows:
| Depth | Weight | Cum Weight in Air | Weight in Mud |
| 10,400 ft – 8,330 ft | 97.3 kips | 97.3 kips | 82.6 kips |
| 8,330 ft – 6,575 ft | 82.5 kips | 97.3 + 82.5 = 179.8 kips | 152.6 kips |
| 6,575 ft – 2,478 ft | 178.2 kips | 179.8 + 178.2 = 358 kips | 303.9 kips |
| 2,478 ft – 623 ft | 87.2 kips | 358 + 87.2 = 445.2 kips | 378 kips |
| 623 ft – surface | 33.3 kips | 445.2 + 33.3 = 478.5 kips | 406.7 kips |
To ensure that the selected design meets the safety factor for tension of 1.6 we divide the cumulative weight of each pipe section into the tensile rating of each grade. We then come up with a design factor:
- 53.5# C-95 1220 kips / 82.6 kips = 14.8
- 47# L-80 905 kips / 152.6 kips = 5.9
- 43.5# C-75 776 kips / 303.9 kips = 2.547#
- L-80 905 kips / 378 kips = 2.453.5#
- C-95 1220 kips / 406.7 kips = 3.0
From these results we can see that the design exceeds the tensile safety factor of 1.6.
Biaxial Effects
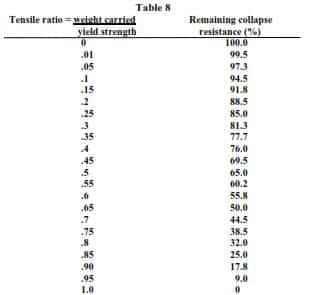
Finally we need to check the weakest grade for biaxial collapse correction. Grade C-75 43.5# is the weakest grade, carrying a buoyant load of 303,900 lb. By dividing this load by the yield strength of 942,000 lb we can see:
303.9 kips / 942 kips = 0.32
Looking at below table we see that the collapse reduces to 79% of its original value of 3750, or 2963 psi. Therefore, rechecking the collapse safety factor for that casing grade at that depth of 2478 ft we get:
2963 psi / [2478 ft x (73 pcf/144 in2/ft2 )] = 2.3,
then since the safety factor is still greater than 1.125, the biaxial effect on collapse did not change the casing design.
Go Back To: Selection Of Casing Weights, Grades and Couplings