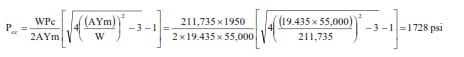We can define Biaxial Casing as the combination of stresses due to the weight of the casing and external pressures which is also referred to as ‘biaxial stresses’. Biaxial stresses can reduce collapse resistance of the casing and must be accounted for in designing deep wells. This article is a part of Our Casing Design Manual.
The collapse resistance, Pcc under tensile loading is given by the following formula:
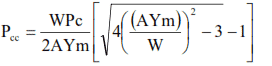
Where
- Pcc= Minimum collapse pressure under axial tension stress (psi)
- Pc = collapse resistance with no tensile load (psi)
- W = weight supported by the casing (lb)
- Ym = average yield stress of steel (psi) with zero load
- A = cross sectional area.
Biaxial loading generates forces within the surfaces of the casing which reduce the casing collapse but increase its burst resistance.
This equation can be represented in tabular form, showing the percentage reduction in collapse resistance for a given unit weight carried by the casing, see below.
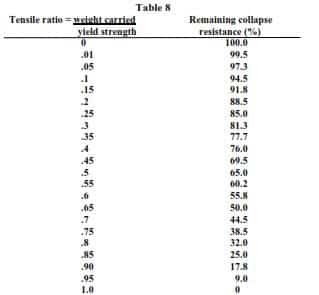
To use above Table, determine the ratio between the weight to be carried by the top joint of the weakest casing and the yield strength of the casing. Then from the table determine the corresponding reduction in collapse strength.
Example to explain the casing biaxial design :
A 13-3/8” 68# K-55 casing string with an average yield strength 1,069,000 lb, weighs 250,000 lb in air and is to be run in a well that contains 75 pcf mud. The ID of the casing is 12.415 in.
What is the corrected weight of the casing and what is the collapse rating reduced due to biaxial loading / biaxial stresses?
Solution:
Corrected weight (W) is: 250,000 lb [1 – (75/490)] = 211,735 lb
The biaxial effect on the collapse rating of the pipe is: 211,735/1,069,000 = 0.198 and looking at Table 8 on page 41 for this ratio we can see that the collapse resistance needs to be multiplied by a 0.885 correction factor.
So instead of a collapse rating of 1950 psi for this casing, it is actually 1726 psi once the biaxial effect is included.
We can also solve this by using the above equation.
- W = 211,735 lb
- Pc = 1950 psi
- Ym = 55,000 psi
- A = πt(OD-t) = 19.435 in .