It was a very important parameter of reservoir absolute permeability in reservoir evaluation and production prediction for log analysts. So, acquiring reservoir absolute permeability information of target intervals was important for the field development planners, especially in tight sandstone gas zones, but it was also a challenge.
At present, many methods have been proposed. Many models & formulas have been established between rock porosity and permeability from core samples to calculate reservoir absolute permeability from well log data. Still, they were all simply correlations between limited core porosity and permeability and didn’t have wide applicability, especially in tight sandstone gas zones, because of the poor correlation (see Figure 1). From Figure 1, we can see clearly that the overwhelming majority of core samples’ permeability was lower than 1.0×10-3 μm2. They were only slightly higher because they came from the thin sand with high porosity and permeability.
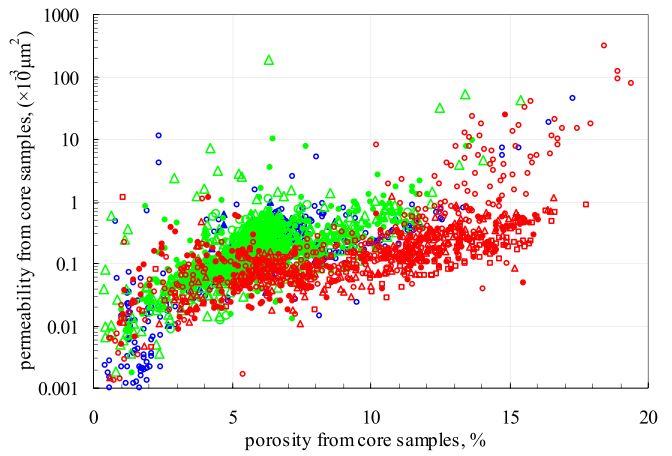
In the same time, the relationships between rock porosity and permeability were different in different wells. In this condition, it was difficult to establish only a model and use it in whole wells. Maybe this problem could be resolved by partition scale division methods, such as establishing different relationships in different zones. However, this would make the well-logging engineers spend too much time calculating continual reservoir permeability, which was unsuitable.
To resolve all these problems, two methods were proposed to calculate reservoir permeability consecutively by integrating the NMR imaging log and capillary pressure data, and their applicability was compared. At last, the Swanson parameter model was recommended for use. The practical application illustrated that the Swanson parameter model was usable in tight sandstone gas zones and conventional formations with high absolute permeability.
Definition:
Absolute permeability is the measure of the ability of a fluid to flow through the permeable rock. In the case of absolute permeability, it is assumed that only one type of fluid is present in the pore spaces of a rock. This value of absolute permeability is then used to calculate the relative permeability of a rock, in which fluids are considered to be flowing in the pore spaces of rock simultaneously.
Equations & Formula For Absolute Permeability Calculation:
The most widely used equation in oil and gas fields to calculate permeability in porous media is the Darcy equation (Check also Darcy Low), which is given as Darcy’s equation for linear flow below:
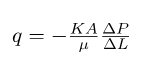
A lab experiment is performed to calculate the absolute permeability of a fluid by flowing fluid of known viscosity through a core sample at a determined flow rate and differential pressure. After obtaining all the requirements, it is put in the absolute formula equation above, and a permeability value is calculated. The simple setup of this experiment is shown in Figure 1:
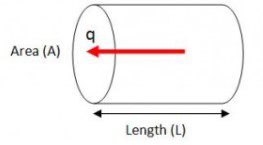
In equation:
- q = flow rate, cc/sec
- k = permeability, Darcy (D)
- A = cross-sectional area to flow, cm2
- μ = viscosity, cp
- Δ p = pressure difference, atm
- Δ L = Length of fluid path, cm
In Field Unit
The Darcy Equation formula For Absolute Permeability that is written above, when expressed in field units, becomes:
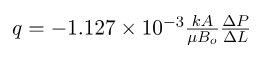
Where;
- q = flow rate, STB/day
- k = permeability, (mD)
- A = cross-sectional area to flow, ft2
- μ = fluid viscosity, cp
- Δ p = pressure difference, psi
- Δ L = Length of fluid path, ft
The Formula
From the equation & formula above, absolute permeability can be expressed as:
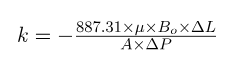
If the flow is 3-dimensional, the following are the signs representing each axis of the flow:
- kx = Horizontal permeability in the direction of the x-axis.
- ky = Horizontal permeability in the direction of the y-axis.
- kz = vertical permeability in the direction of the z-axis.
kx and ky show the permeabilities of the parallel bedding of rock pore spaces, while kz shows the perpendicular permeability of a vertical bedding plane. There is a lot of variation between vertical permeability and horizontal permeability, and this variation of permeabilities along different planes is called “Anisotropy”. This concept is significantly important when dealing with reservoir modeling. Most of the time, the values of kx and ky are quite close to one another; however, the values of kz differ significantly.
Average Permeability:
When dealing with a reservoir having different layers of formation, each layer has a different value of absolute permeability. Then, the value of the permeability must be averaged so that it should represent the permeability of the whole reservoir. There are two different types of methods to calculate average permeability: the thickness-weight average method and the geometric mean method.
Thickness-weight average method:
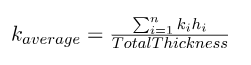
Where;
- kavg = Average permeability
- k = Permeability of layer
- h = thickness of layer
Geometric mean:
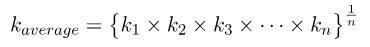
Factors Affecting Permeability:
The ability of the fluid to flow through the pore spaces of rock depends on many factors as stated below:
- Size, shape, and distribution of the grains along the rock.
- Formation’s porosity (φ).
- Formation type.
- Type of fluid and its pressure behavior in the formation.
Above are the factors affecting the absolute permeability relationships in the rock. Figures 2, 3, and 4 illustrate the effect of different grain arrangements in formation and their effect on permeability.

Range of Permeability Values:
Permeability changes significantly in the rocks ranging from 1 nano Darcy (nD) (1*10-9 D) to 1 micro-Darcy (μD) (1*10-6) for clays, shales, and granites that contribute towards the formation of cap-rock or make a reservoir rock having a permeability of several Darcie’s making it a good reservoir to permit fluids. One mD is considered a threshold below which a rock is not considered a reservoir unless there are some unusual conditions, like the reservoir being a fractured formation, etc. Classification of permeabilities for reservoir rock is enlisted in the table below:
Table 1: Classification of Reservoir Permeability:
| Permeability Value (mD) | Classification |
| ˃1000 | Exceptional |
| 100 – 1000 | Very High |
| 10 – 100 | High |
| ˂10 | Fair |
Determination of Absolute Permeability:
As described earlier, permeability is measured in a lab by flowing the fluid of known viscosity through the core sample, calculating the pressure drop from both ends and estimating the flow rate. We get the permeability after putting all the values in the Darcy equation. However, the type of fluid affects this calculation a lot. Gaseous fluid and liquid must be differentiated because measurements regarding liquid flow are easy as the requirement for incompressibility of the fluid and laminar flow are met at the surface conditions. But in the case of gaseous flow, there are two types of complications involved in the process:
- The compressibility factor of gas is the first complication. Gas molecules will flow through the core more slowly at the entrance point than they will travel at the exit point when measured in volume per time. This factor is not incorporated in Darcy’s equation, so that equation must be modified according to that.
- Secondly, at the lower pressure of the gas, fewer gas molecules will be present in the smaller pore spaces of the rock, thus causing an overestimation of the permeability values. This effect is called the “Klinkenberg Effect” or “Slippage”. This problem is resolved when the pressure increases and more molecules per unit volume are confined into the pore spaces of the rock. This issue also does not arise in the case of liquids because liquids are denser than gases.
Advanced Formula & Calculations For Absolute Permeability
Classical models of calculating absolute permeability by using nuclear magnetic resonance (NMR) log
Since the nuclear magnetic resonance technology was introduced to well logging industry, it exhibited a unique aspect, from which two classical models the SDR model and the Tim-Coates model, were proposed to calculate permeability from NMR log data; these two models were expressed as:
K = C1 × φm1× Tn1
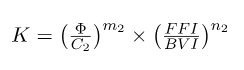
Where:
- K was rock absolute permeability in 10-3μm2
- φ stood for rock total porosity in %
- T2lm was the geometric mean value of NMR T2 distribution in ms
- FFI stands for the free fluid bulk index in %
- BVI was bound fluid (often bound water) volume in %, m1, n1, C1, m2 n2, and C2 were model parameters, which could be gained from core samples data; when core samples were absent, they were assigned to 4, 2, 10, 4, 2, 10 separately.
With the analysis of the SDR model and Tim-Coates model, some difficulties could be found, such as the undefined parameters being too much, and we also must understand reservoir porosity, FFI, and BVI. In practical application, determining the value of FFI and BVI depended on the value of the NMR T2 cutoff, which divided the NMR T2 distribution into two parts, equaling FFI and BVI separately. However, determining the value of the T2 cutoff was a general problem.
No optimum methods have been proposed to gain T2 cutoff from NMR T2 distribution, so we assigned its value as 33 milliseconds in sandstone and 92 milliseconds in carbonate rock. In practical application, we found that it was not always applicable, especially in low porosity and low permeability gas zones, with little pore space often occupied by exploitable gas, which would be considered as bound water, and the reservoir porosity also would be lower than the true value because the hydrogen index of gas was lesser than water.
So, the clue must be changed. In this paper, based on the fact that NMR T2 distribution and mercury-injection capillary pressure curves all reflected the reservoir pore structure, we proposed novel methods to calculate reservoir absolute permeability by combining NMR log and capillary pressure data in tight sandstone gas zones, which could avoid the difficulties of gain too much reservoir parameters in classical models.
Absolute Permeability References:
- Absolute Permeability. 2021. drilling formulas
- Comparison Study of Models for Calculating Absolute Permeability Using Nuclear Magnetic Resonance Imaging Log Technology in Tight Sandstone Gas Zones
Thanks for this great blog.
I didn’t know that.
Right on my man!