Hydrostatic Pressure Formula In Oil And Gas

Hydrostatic pressure in oilfield drilling is the pressure that a fluid exerts due to the weight of the fluid column above it. This pressure varies with the depth and density of the fluid. It’s present at all points below the fluid surface, regardless of whether the fluid is a liquid or a gas. For instance, the weight of the air creates atmospheric pressure, which is about 1 atm = 14.7 psi at sea level. However, the atmospheric pressure decreases as you go higher above sea level. Regarding hydrostatic pressure in oil and gas, the formula is determined by multiplying the fluid density by the true vertical depth.

Oilfield problems often involve determining the pressures that are being exerted on the casing pipes, completion tools, or tubing. In the case of directional drilling, the hydrostatic pressure formula in oil and gas depends on the actual or true vertical depth, not the measured depth. For instance, a deviated well may have a measured depth of 12,000 feet, but the true vertical depth may only be 9,000 feet. It’s important to note that hydrostatic pressure in a well solely depends on true vertical depth.

Hydrostatic Pressure Formula In Drilling

We can generally use the below formula to determine the hydrostatic pressure:

P_h = W x H

Where:

• P_h= Hydrostatic Pressure
• W = Fluid Weight (Gas or Liquid)
• h = The actual Vertical Depth

The formula indicates that the P_h depends mainly on the following:

• Fluid density refers to the mass of a fluid per unit volume and can also be expressed as specific gravity (γ). In the American system, fluid weight is more commonly used to specify fluid density. It is measured in units such as PPG or lb/ft3.
• Depth

Formula In API Units

P_h in (PSI) = Pressure gradient in (PSI/FT) × TVD (FT)

Hydrostatic Pressure P_h in (PSI)= 0.052 X Density in (PPG) X TVD (FT)

P_h in (PSI)= 0.006944 X Density in (LB/FT³) X TVD (FT)

• P_h= Hydrostatic Pressure
• TVD: True Vertical Depth
• 0.052: Conversion factor (PSI/FT per LB/GAL) can be calculated as follows:
  • One cubic foot contains 7.48 US gallons.
  • Therefore, a fluid that weighs 1 pound per gallon (PPG) is equivalent to 7.48 pounds per cubic foot.
  • If we consider the pressure exerted by one foot of this fluid over the area of its base, we can calculate the conversion factor of 0.052 psi/ft per lb/gal = 7.48 Ibs / 144 Sq.ins
• 0.006944: Conversion factor (PSI/FT per LB/FT3)
  • One square foot equals 144 inches
  • 1/144 = 0.006944 to convert from 1 square inch to 1 square foot.

Hydrostatic Pressure Formulas For Oil & Gas Drilling In Metric Unit

P_h in (KG/M²)= Density in (KG/M³) X TVD (M)

Hydrostatic P(PASCAL)= 9.81 X Density(KG/M³) X TVD(M)

P_h in (BAR)= 0.0000981 X Density in (KG/M³) X TVD (M)

P_h in (ATM)= 0.000096816 X Density in (KG/M³) X TVD (M)

Where:

• P_h= Hydrostatic Pressure
• TVD: True Vertical Depth
• 9.81: Conversion factor — 1 KG/M² = 9.81 Pascal.
• 0.0000981: Conversion Factor — 1 KG/M² = 9.81 x 10^-6 BAR.
• 0.000096816: Conversion Factor — 1 KG/M2 = 9.81 X 9.8692 X 10^-6 ATM

Fluid Gradients

There are different formulas & ways to specify a fluid’s weight, making it difficult to use when calculating hydrostatic pressure in oil and gas. Instead, hydrostatic pressure in drilling is usually defined by a fluid gradient to avoid the need to convert fluid weight and depth into similar units. The fluid gradient represents the pressure exerted per unit depth and is derived by manipulating the units. For instance, let’s consider 38° API oil, which has a fluid weight of 52.06 LB/FT³. This can also be expressed as 52.06 LB/FT²/FT or LB/FT² per FT. The units LB/FT² are units of pressure and can be converted to lb/in by multiplying by the conversion factor 0.006944 FT²/IN². By doing the math, we get the following:

52.06 LB/FT³× .006944 FT²/IN²= 0.362 LB/IN²/FT= 0.362 PSI/FT

If the fluid weight is in LB/GAL, multiplying the fluid weight by 0.05195 gal/(FT.IN²) will give the fluid gradient. The engineering tables provide a list of fluid gradients in different units to make calculations easier. Therefore, we can calculate the P_h by multiplying the fluid gradient by the depth.

P_h (PSI)= Fluid Gradient (PSI/FT)× TVD (FT)

Fluid Gradients of Mixtures

At times, it becomes essential to determine the fluid gradient of a mixture of multiple liquids, for instance, a mixture of oil and water. To calculate the fluid gradient of such a mixture, you need to multiply the fluid gradient of each fluid by its percentage of the total, add the outcomes together, and divide the sum by 100. To express this concept in a mathematical formula:

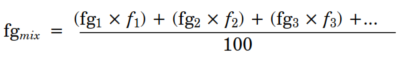
Where:

• fg_mix= fluid gradient of the mixture (psi/ft)
• fg= fluid gradient of liquid n (psi/ft)
• fn= percentage of liquid n

Slurry Gradients

In many service operations such as hydraulic fracturing, gravel packing, etc., finding a pressure gradient for a fluid-sand mixture is necessary. Adding the weights of fluid mixtures together does not yield accurate results. The sand displaces some of the fluid volume and must be accounted for in the calculations. To determine the weight of a sand slurry, use the following formulas:

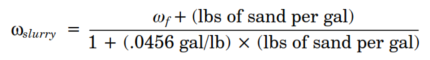
Where:

• ω_slurry = weight of sand slurry (lb/gal)
• ω_f= weight of fluid (lb/gal)

OR

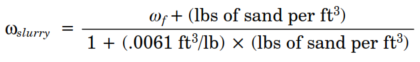
Where:

• ω_slurry = weight of sand slurry (lb/ft³)
• ω_f= weight of fluid (lb/ft³)

Gas Gradients

As mentioned earlier, gases also exert hydrostatic pressure. Unlike liquids, gas will compress under pressure, and hence, its density will increase. In other words, more gas will fit into a fixed volume under high pressure than under low pressure. Since hydrostatic pressure depends on density, gas will exert greater hydrostatic
pressure as the applied pressure increases. Temperature also affects the density of a gas. As temperature decreases, gas density increases. As, such gases pose a unique challenge when they are present in a well. The bottom hole pressure of a gas column is found as follows:

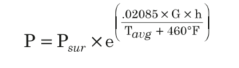
Where:

• P = pressure @ desired depth (psi)
• P_sur = surface pressure (psi)
• e = natural logarithm base = 2.71828
• G = gas gravity
• h = true vertical depth (ft)
• T_avg = average well temperature (°F) = (surface temp + temp @ depth)/2

Gas gravity is the gravity of the gas compared to air. Some common oilfield gas gravities are:

• Air = 1.000
• Carbon Dioxide = 1.529
• Injected Dry Natural Gas = .650
• Methane = .554
• Nitrogen = .967
• Produced Natural Gas = .850
• Propane = 1.554

The oil and gas formulas above apply to gases only; meanwhile, some gases, such as CO2, are normally liquids under high pressure and must be treated as such to determine hydrostatic pressure in drilling.

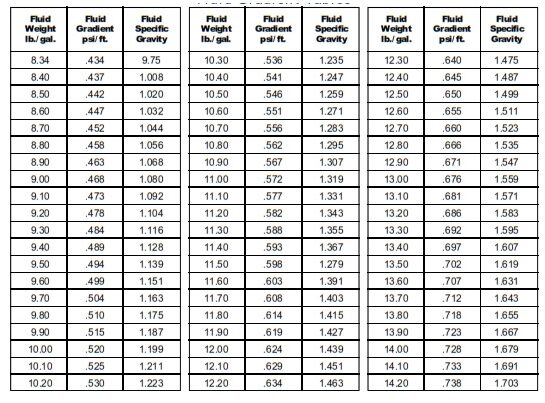
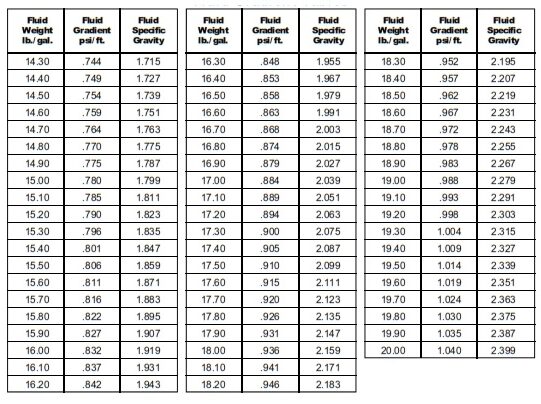
Fluid Gradients Tables

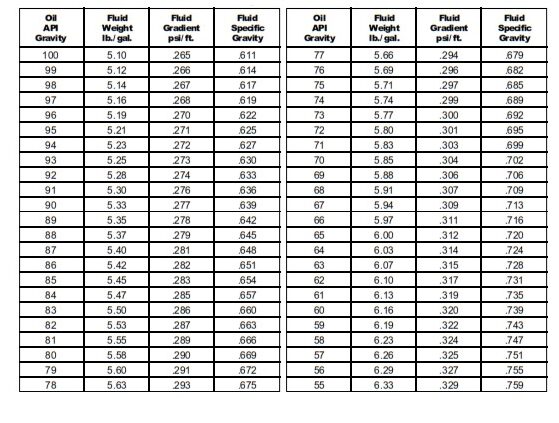
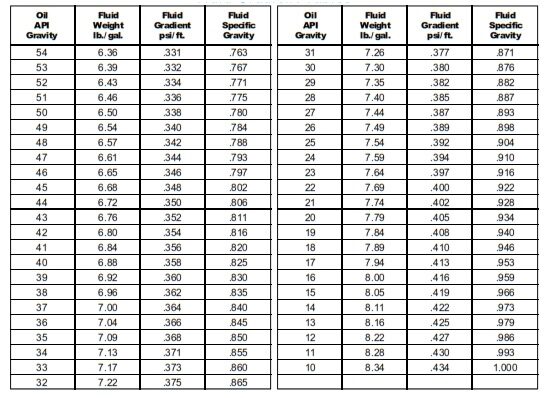
Download Hydrostatic Pressure Formula Excel Sheet For Oil & Gas

Download Calculation Sheet

Example 1

What is the hydrostatic pressure 1,000 FT below the surface in a well filled with 14 lb/gal drilling fluid?

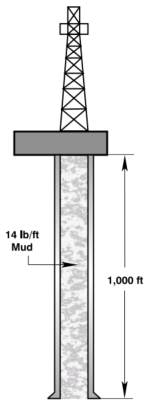
• Fluid density: 14 lb/gal
• Depth: 1,000 ft

Using the “Fluid Gradients” tables above, the fluid gradient of 14 lb/gal fluid is 0.728 psi./ft. Therefore, the hydrostatic pressure is:

P = Fg × TVD = 0.728 psi/ft × 1,000 ft = 728 psi

Note that the hydrostatic pressure in drilling does not depend on the tubing or casing size. Hydrostatic pressure depends only on the fluid density and the depth. If a well is not full, determine the P_h using the true column height of the fluid.

Example 2 For Hydrostatic Pressure Formula In Oil & Gas

Calculate the hydrostatic pressure at the bottom of a 5,000 ft well considering the following:

• The fluid level is at 1,275 ft.
• The well fluid is 15° API oil.

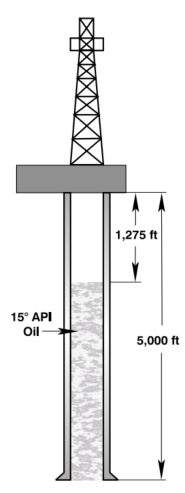
Solution:

From the “Fluid Gradients” table: F_g = .419 psi/ft

The true vertical height of the fluid column is: h = 5,000 ft – 1,275 ft = 3,725 ft

Therefore: P = 0.419 psi/ft × 3,725 ft = 1,561 psi

Hydrostatic Pressure Formula In Oil & Gas – Example 3

Given the following well conditions,

• Fluid (CMT): 800 ft of 15 ppg
• 5,600 ft of 9 lb/gal water
• Well Depth: 6,400 ft
• Pump Pressure: 1,450 psi

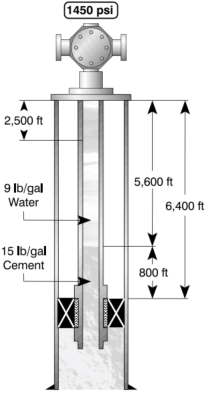
Determine the following:

1. The total bottom hole pressure.
2. The total pressure at the surface.
3. The total pressure at 2,500 ft.

Solution:

From the “Fluid Gradients” tables:

• F_gc =0.780 psi/ft
• F_gw = =.468 psi/ft

Bottom Hole Pressure

Hydrostatic pressure due to cement slurry:

P_c = fg_c × h_c = 0.780 psi/ft × 800 ft = 624 psi

Hydrostatic pressure due to water:

P_w = fg_w × h_w = 0.468 psi/ft × 5,600 ft = 2,620.8 psi

Total hydrostatic pressure in drilling:

P_hydro = P_c + P_w = 624 psi + 2,620.8 psi = 3,244.8 psi

Total bottom hole pressure:

P_total = P_app + P_hydro = 1,450 psi + 3,244.8 psi = 4,694.8 psi

Total Surface Pressure

Since there is no hydrostatic pressure at the surface, the surface pressure is the applied pressure of 1,450 psi.

Pressure at 2,500 ft:

At 2,500 ft there is no cement, so only the water is considered.

Hydrostatic pressure at 2,500 ft:

P_hydro = fg × h = .468 psi/ft × 2,500 ft = 1,170 psi

Total pressure at 2,500 ft: Adding P_app to P_hydro

P_total= 1,450 psi + 1,170 psi = 2,620 psi

Example 4

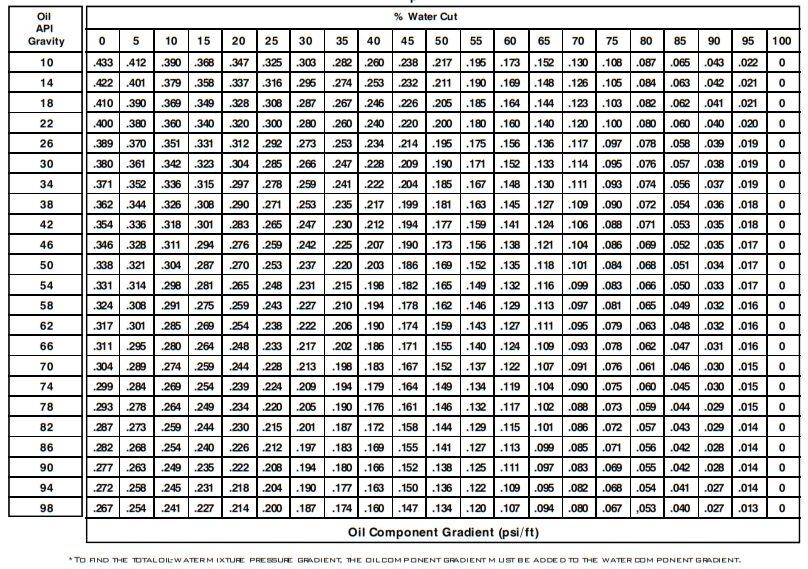
What is the fluid gradient of an oil-water mixture that is 60% water cut, if the water weighs 9.2 lb/gal and the oil is 35° API?

Solution:

From the “Fluid Gradients” tables:

fg_w = 0.478 psi/ft

fg_o = 0.366 psi/ft

Fluid gradient of the mixture:

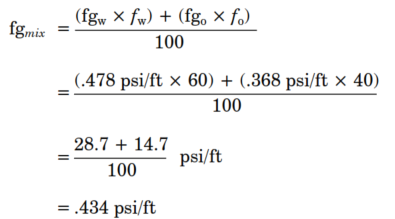
Using the “Fluid Gradients of Oil-Water Mixtures” table above:

fg_mix = water component + oil component = 0.287 psi/ft + 0.147 psi/ft = 0.434 psi/ft

Example 5

Calculate the pressure in a 1,500 ft well filled with 9.0 ppg water to which 3 pounds of sand per gallon is added.

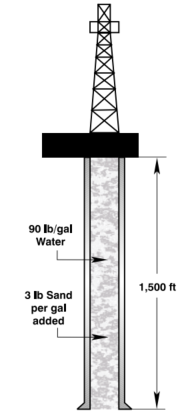
Solution:

Slurry weight:

Multiply the weight by the conversion factor 0.05195 gal/(ft.in²) to determine the slurry pressure gradient

fg_slurry = 10.56 lb/gal × 0.05195 gal/(ft.in²)= 0.548 psi/ft

Hydrostatic pressure: P = 0.548 psi/ft × 1,500 ft= 823 psi

Example 6

Determine the bottom hole pressure of a well under the following conditions:

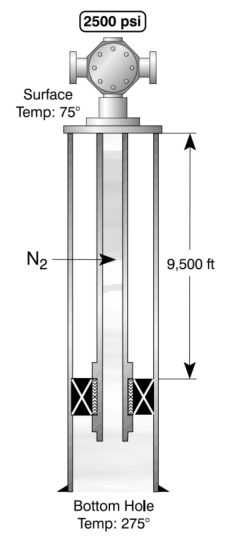
Well Data:

• Depth: 9,500 ft
• Bottom Hole Temp.: 275°F
• Surface Temperature: 75°F
• Surface Pressure: 2,500 psi
• G_N2= 0.967

Solution:

Average well temperature:

Bottom hole pressure:

References:

• Schlumberger Completions Hydraulics Handbook
• Aberdeen Well Control Manual