D is an exponent which, relating drilling penetration rate to weight on bit per unit hole diameter, measures the formation’s ” drillability “. There were several attempts to link the drilling parameters to generate a measure of drillability. The best known was by Jorden and Shirley *, who demonstrated empirically that in homogeneous shale formations, and with all other factors being equal, the drilling penetration rate is proportional to the rotation rate of the drilling bit.
D Exponent Calculation
Bingham
Bingham proposed a generalized drilling rate equation to interrelate all relevant drilling parameters (1964):
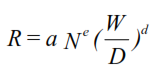
Where:
- R = ROP (ft/hr)
- N = rotary speed (rev/sec)
- e = rotary speed exponent
- W = WOB (lbs)
- D = bit size (ft)
- a = matrix strength
- d = formation drillability exponent
Bingham absorbed changes in ΔP ( differential pressure) in the constant a.
Jorden and Shirley
Jorden and Shirley demonstrated empirically that in homogeneous shale formations, and with all other factors being equal, the penetration rate is proportional to the rotation rate of the drilling bit.
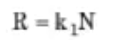
- R = ROP (ft/hr).
- N = rotary speed (rev/sec).
- K1 = Proportionality constant.
Jordan & Shirley also showed empirically that the penetration rate depends on the weight on bit and hole size according to an exponential relationship:
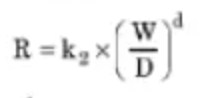
D is considered the drilling d exponent. It was shown, still empirically, that combining the two above equations into one:
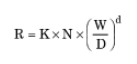
- W = WOB (lbs).
- D = bit size (ft).
- K2 = Proportionality constant.
It gives a good approximation of the behavior of a real system in practice.
D exponent Derivation
Given that the utility of such a relationship is to compare the drillability of similar formations in similar circumstances rather than to establish the absolute value of a well-defined parameter, the equation is simplified by dropping the constant. The relative drillabilities of similar formations in which only the penetration rate, weight on bit, rotation rate and hole diameter vary is then given by the value of “d exponent” in the equation

Given again that the objective is to make comparisons rather than establish absolute values, the units in which drilling penetration rate, weight on bit, rotation rate, and hole diameter are expressed do not affect the final result. When working in oilfield units, in which penetration rate is measured in ft/hour, weight on bit in lbs, rotation rate in rpm, and hole diameter in inches, the convention has grown to insert factors to convert diameter to feet, to make the time units consistent and to convert the weight on bit units into lbs x106.
Conventionally thus
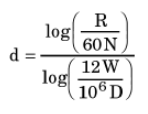
Where:
- R = ROP (ft/hr)
- N = RPM (rev/min)
- W = WOB (lbs)
- D = bit size (ins)
Corrected D Exponent Calculation:
It has been found that the “d exponent” can additionally be adjusted for drilling fluid density variations. This gives the compensated d exponent, “dc“. Rehm and McClendon (1971) proposed the corrected d exponent to account for changes in mud weight.

Final Words
Although the connection cannot be mathematically justified, using this compensated d (“dc“) exponent has proved advantageous. These exponents were developed for application in homogenous shale intervals. They are less reliable in variable lithology, sandstone, and limestone. However, a sealing cap rock is likely a shale, so it does have relevance. Additionally, the equation was specifically developed for Gulf Coast conditions where drilling shale is the norm; it should be used cautiously in other areas.
Other algorithms that require significant raw data processing have been developed, such as Geoservice’s Sigmalog, Baroid’s Log Normalised Drilling Rate (LNDR), and Anadrill’s Instantaneous Drilling Evaluation Log (IDEL) or A-exponent. These and others may be provided as a standard or additional Mud Logging service.
Useful Notes:
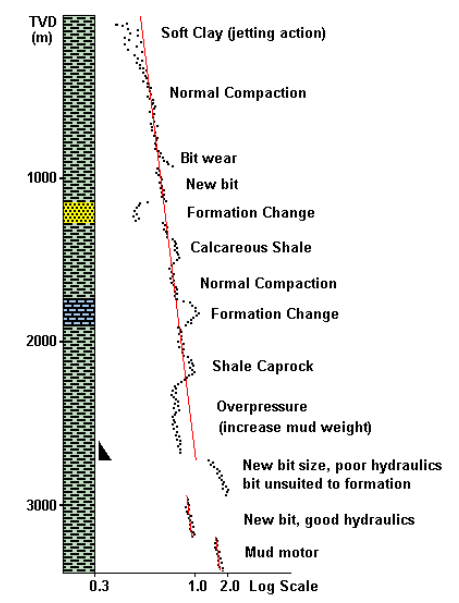
- When (R/60N)< 1, then (R/60N) varies inversely with ROP, and so the d Exponent varies inversely with ROP.
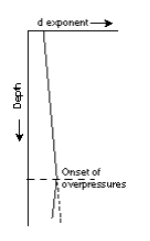
- When drilling constant lithology, the d exponent will increase with depth, compaction, and ΔP.
- The d exponent is not compensated for mud weight, SPP (i.e., hydraulics), and bit wear.