
For many years, drilling engineers have known that hydraulics play an essential role in cleaning the face of the formation so that a bit can drill faster. This first became evident when larger mud pumps increased the drilling rate because more mud was being pumped through the large throat of the regular circulation bit. Jet bits were developed to improve the jetting action of the high mud velocities at the drilling bit. In addition, features such as extended nozzles and varying the number of nozzles affected the drilling rate.
Much speculation has been made concerning hydraulics’ role in solids removal. For example, do high-impact forces clean the hole more effectively than maximum jet velocities? The critical point in this speculation is the attempt to develop the “perfect” cleaning mechanism such that a drilled rock fragment is removed virtually instantaneously after it is drilled. As yet, industry personnel does not agree on the perfect cleaning technique.
Many attempts have been made to optimize certain bit hydraulics variables to cause perfect hole cleaning. The variables most commonly optimized are impact force, hydraulic horsepower, and jet velocity. In some cases, any of these variables, when optimized, will clean the hole, whereas in other cases, one is more effective than the others. In some cases, none are efficient.
Drilling Bit Jet Nozzles Optimization – Max Impact Force
Laboratory and field studies have shown that cross-flow beneath the face of the bit is the most effective parameter in hole cleaning. Cross flow is maximum when an impact force is maximum. To optimize hydraulics, the pressure relationships throughout the well must be defined. The total pump pressure (Pp) is equal to the sum of all friction pressures (PF) and the bit pressure drop (Pa):
PP = PF + PB
In addition, by observing that PF is proportional to the velocity:
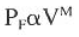
Where:
- M = flow exponent, usually taken as 1.75
It can be said that:
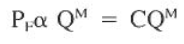
Where:
- C is a constant representing mud properties and wellbore geometry.
Rearranging the above equations:
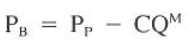
Jet impact force was defined previously as follows:
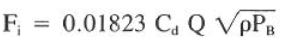
By substituting Eq. 5 into Eq. 6, the following expression is established:
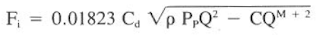
Using calculus, Eq. 7 can be maximized and resolved into Eq. 8:
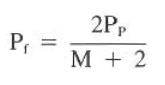
Realizing that M is approximately 2, the equation reduces to 0.5 Pp, the familiar 50% of pump pressure expended at the bit for optimum impact conditions.
To summarize the above, our concept of the max impact force method depends on the best condition to clean the well when the force provided by the jets is the maximum. Based on the mathematical solution, this condition occurs when bit nozzles and circulation rate are properly selected to create a pressure drop across the bit equal to 50% of the total pump pressure.
For example, if the maximum expected pressure is 3,000 psi, you need to select the flow rate and the bit nozzles, which will generate 1,500 psi (50% of 3,000 psi) pressure drop across the bit and leave 1500 psi (50% of 3,000 psi) for the system pressure loss.
Bit Hydraulics – Max Hydraulic Horsepower
The hydraulic horsepower equation can be optimized similarly, resulting in the following equations:
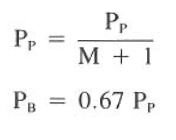
The above equation is developed if M is set equal to 2 so that Pf = 1/3 Pp.
This Jet optimization according to maximum hydraulic horsepower is based on the concept that the best condition to clean the well is when the hydraulic horsepower at the bit is the maximum. Based on the mathematical solution, this condition occurs when bit nozzles and circulation rate are properly selected to create a pressure drop across the bit equal to 67% of the total pump pressure.
For example, if the maximum expected pressure is 3,000 psi, you need to select the flow rate and the bit nozzles, which will generate 1,950 psi (67% of 3,000 psi) pressure drop across the bit and leave 1050 psi (33% of 3,000 psi) for the system pressure loss.
Jet Nozzles Optimization – Graphical Method.
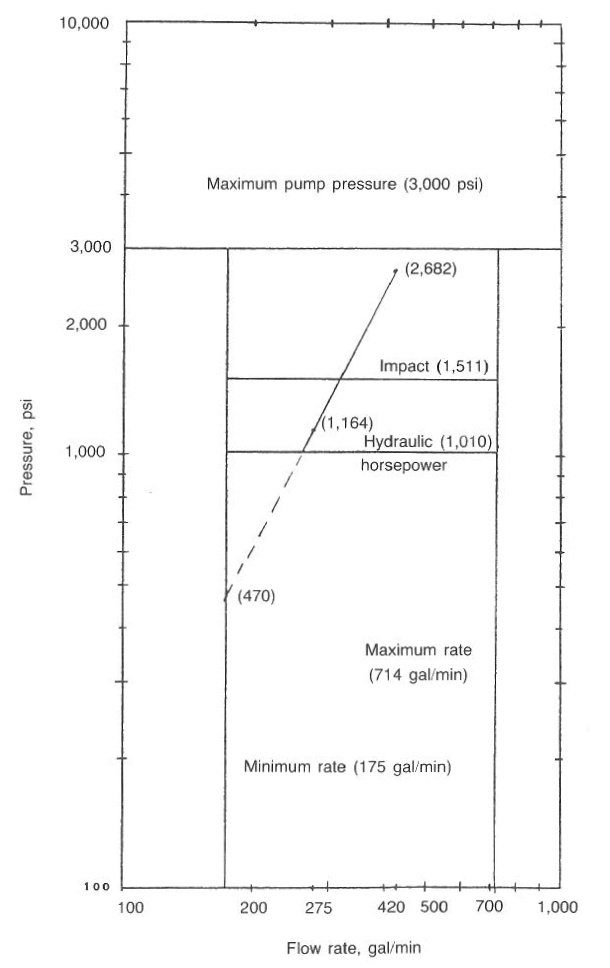
The most convenient method for selecting proper jet sizes for bit hydraulics optimization is the graphical approach shown below. The maximum possible flow rate is based on pump horsepower and pressure limitations. The minimum flow rate is based on acceptable annular velocities for cuttings removal or minimum pumping rates from mechanical restrictions. These two lines are connected by the desired friction pressure losses, usually 50% for impact force or 33% for hydraulic horsepower criteria. The most accurate method is to determine M from two flow rates on the given well and compute the optimum friction pressures using the above Eqs.
After the graph is constructed, plot the two friction pressures resulting from the test rates, determined by subtracting the computed bit drop from the pump pressure. Draw a line through the two points until it intersects the path of optimum drilling hydraulics. The intersection point determines the desired flow rate,
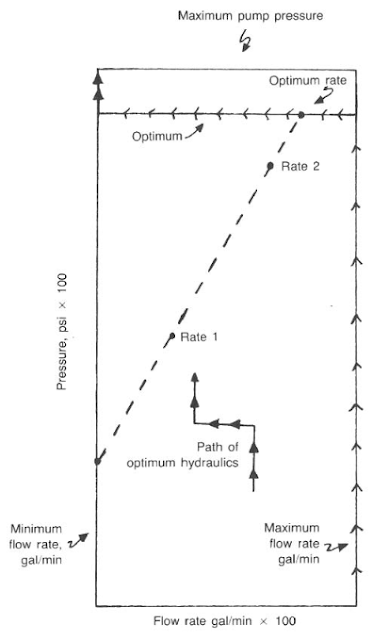
which can be substituted into Eq. 18.54 to compute the desired area for the jet nozzle:
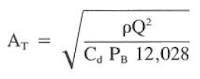
Example For Bit Hydraulics Calculations
A drilling engineer intends to optimize the bit hydraulics on a well with the following characteristics. Select the proper jet sizes for the impact force and hydraulic horsepower methods:
- Pump rate # 1 = 200 gal/min = 3,000 psi
- Pump rate #2 = 275 gal/min = 1,300 psi
- Pump horsepower = 1,250 hp
- Surface pressure = 3,000 psi (maximum)
- Mud weight = 13 Ib/gal
- Jet sizes = three 17/32nds
- Minimum acceptable annular velocity = 70 ft/min
- Minimum pump rate = 175 gal/min
- Hole geometry:
- 4 1/2 in.drill pipe
- 7 in. drill collars
- 8 1/2 in.annulus
Solution:
1. Determine the maximum possible flow rate as the upper-end constraint
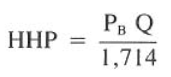
Q = 714 gal /min
2. Determine the minimum flow rate. The lower-end constraint is based on minimum pump rates or annular velocity. The velocity of 70 ft/min is converted to a flow rate:
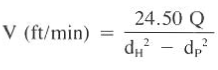
70 ft/min = 24.5 x Q / (8.5^2 – 4.5^2)
Q = 148 gal/min
Since the pump’s idle rate of 175 gal/min > 148 gal/min, the minimum flow rate is 175 gal/min.
3. The friction pressures for each pump rate in bit hydraulics are calculated as follows:
Pp = PB + Pr
Pr = Pp – PB
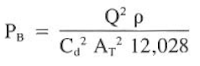
PB (rate # 1) = ( (420^2) (13) ) / ( (0.95^2) (12,028) ( 3/4 π (17/32) ^2) ) = 317 psi
Pr (rate #1) = 3,000 – 317 = 2,682 psi
Pr ( rate # 2) = ( (275^2) (13) ) / ( (0.95^2) (12,028) ( 3/4 π (17/32) ^2) ) = 736 psi
Pr (rate #1) = 1,300 – 136 = 1,164 psi
4. The slope (M) can be computed graphically from below Fig.
or with the below Equation:
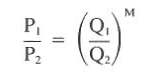
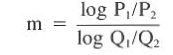
m = log (3,000/ 1,300) / log (420/275) = 1.97
5. Use the below Eqs. to determine the optimum friction pressure losses for the impact force and hydraulic horsepower methods. Plot the results in Fig. 3.
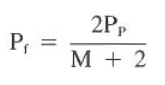
5.1. Max Impact force
Pf = 2 (3000) / (1.97+2) = 1511 psi
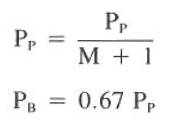
5.2. Max Hydraulic horsepower
Pf = 3000 / (1.97+1) = 1010 psi
6. From the above Fig.3, the optimum flow rates are:
- impact = 315 gal/min
- hydraulic horsepower = 260 gal/min
7. The optimum nozzle sizes in bit hydraulics are computed with the results from step 7 and Eq. 10:
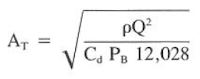
PB(impact) = 3,000 – 1,511 = 1,489 psi
PB(HHP) = 3,000 – 1,010 = 1,990 psi
Max Impact Force
A = ( (13) (315^2) / ( 0.95^2) (1489) (12028) ) ^ (1/2)
A = 0.2825 in2
0.2825 = 3/4 π (x / 32)^2
x = 11.01, so (Use three 11/32nds)
Max Hydraulic horsepower
A = ( (13) (260^2) / ( 0.95^2) (1990) (12028) ) ^ (1/2)
A = 0.2017 in2
0.2017 = 3/4 π (x / 32)^2
x = 9.36 so (Use one 9/32nds and two 10/32nds)
Drilling Bit Jet Nozzles Optimization – Jet Velocity.
The maximum velocity of the fluid moving through the bit jets occurs when a maximum pressure drop is observed at the lowest possible flow rates. The rates are generally based on the slip velocity of the cuttings in the annulus and the mud flow rates required to exceed this velocity. To use Eq.10, the flow rate is established as the minimum possible volume. The line in Fig.2 is extrapolated downward until it intersects the minimum flow rate line. The pressure at this intersection is the value to be substituted into Eq.10. In many deep wells, hydraulics and impact optimization degrade into jet velocity criteria because of the high friction pressures associated with these wells.
Example (Bit Hydraulics)
The last examples were used to calculate optimum jet sizes for the impact force and hydraulic horsepower methods. Using the same data, determine the optimum jet sizes for the velocity method. Do not use jet sizes less than 8/32nds. A 1- or 2-nozzle selection may be necessary.
Solution:
1. Refer to Fig.2 . Extrapolate the friction pressure line until it intersects the minimum rate of 175 gal/min:
Pf = 470 psi
Pp = PB + Pf
PB = Pp – Pf =3,000 – 470 =2,530 psi
2. Determine the jet size:
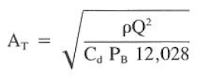
A = ( (13) (175^2) / ( 0.95^2) (2530) (12028) ) ^ (1/2) = 0.120
0.120 = 3/4 π (x / 32)^2
x = 8.8
Use two 9/32nds jet sizes at 175 gal/min.