It will be recalled that the upward velocity of the mud in the annulus between the drill pipe and wall of the hole is an important consideration with that function of drilling fluid of removing drilling cuttings. The usual expression of this annular velocity is in feet per minute.
Annular Velocity Calculations & Formula
This important term must be considered carefully when selecting a flow rate: excessive-velocity opposite open hole promotes erosion, while insufficient one in the larger annulus near the surface can cause inadequate cuttings transport. It is calculated from the following equation:
Annular Volume, bbl/ft = capacity open hole, bbl/ft minus (capacity of drill pipe and displacement of drill pipe, bbl/ft)
Annular Velocity, ft/min = (pump output, bbl/min) / (Annular Volume, bbl/ft)
V = 0.024 x gal/min / (Annular Volume, bbl/ft)
Mud engineers often use other equations forms:
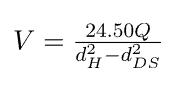
- V = Annular velocity
- Q = mud flow rate, gallmin
- dH = hole diameter, in.
- dDS = drill string diameter, in.
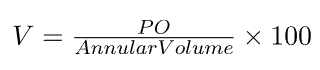
- PO = pump output, bbl/min
- Annular volume, bbl/ ,000 ft
Hole Cleaning
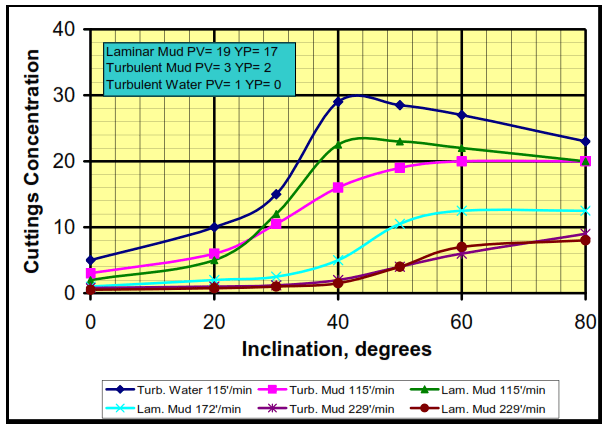
Annular velocity is the variable that will affect hole cleaning the most. Any increase in such term decreases the size of the cuttings bed formed on the low side of the hole and in some cases may prevent it. The three flow rates shown in Figure 1 are 115, 172, and 229 fpm. Each increase in annular velocity shows a corresponding decrease in the total cuttings concentration. Even when a cuttings bed is formed, the annular velocity increases, and the bed is eroded until the system is in equilibrium.
Optimum Annular Velocity
Although any velocity greater than the settling velocity of the largest cutting will theoretically lift all the cuttings to the surface eventually, too low an annular velocity will direct to an undesirably high concentration of cuttings in the annulus. Because of slip, the concentration of drilling cuttings depends on the transport ratio as well as the volumetric flow rate and the rate of cuttings generation by the drilling bit.
